Sigmas de divisores semiprimos

Al igual que con los divisores habituales y los unitarios, los divisores semiprimos pueden dar lugar a funciones SIGMA y TAU.

En la entrada anterior usamos la función div_semi para encontrar y contar los divisores semiprimos de un número. Esta sería la función TAU en este caso. Bastará cambiar ligeramente estas líneas de su código para sumar en lugar de contar o usar potencias:

If essemiprimo(k) And n / k = n \ k Then ‘Es divisor semiprimo
nn = n: e = 0 ‘Posibles exponentes
If repe Then ‘Caso de repetición
While nn / k = nn \ k: e = e + 1: nn = nn / k: Wend
End If
If repe Then m = m + e Else m = m + 1

La última línea cuenta divisores, pero si la sustituyéramos por m=m+e*k^t o m=m+k^t nos serviría para el cálculo de la familia de las SIGMAS, que suman divisores, o sus cuadrados, o también cualquier potencia. Incluso si el exponente es 0, la función seguiría contando en lugar de sumar, es decir, que sería TAU. Estos pequeños cambios en la función div_semi los daremos por supuestos en cada caso.

Funciones SIGMA

Tradicionalmente, estas funciones han sumado los divisores de un número o bien alguna potencia de ellos. En el caso de los semiprimos les añadiremos _S para distinguirlas. Así SIGMA3_S sumará los cubos de los divisores semiprimos. Por ahora no consideraremos las repeticiones.

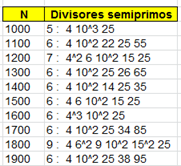
La más sencilla será SIGMA_S, que sumará los divisores semiprimos sin contar repeticiones. En la función div_semi sustituiremos m=m+1 por m=m+k. De esta forma podemos calcular la suma sin repetición si usamos el parámetro repe=0. Por ejemplo, para 330 pediríamos DIV-SEMI(330;0). En la imagen podemos comparar la lista de divisores semiprimos con su suma:

Así que, en este caso, SIGMA_S(330)=141

El resultado, para los primeros números es:

Podemos comparar las dos últimas columnas para verificar las sumas.

Las sumas de la segunda columna están publicadas en  https://oeis.org/A076290

Tambien, si cambiamos ligeramente la versión en PARI, obtendremos los mismos resultados. Esta sería la nueva versión:

sigma_s(n)= sumdiv(n, d, (bigomega(d)==2)*d)
print(sigma_s(330))

Su resultado:

Y para los 20 primeros:

Observamos que coinciden con los publicados.

Hemos intentado buscar números s_perfectos, que coincidan con la suma de sus divisores semiprimos, pero no hemos encontrado ninguno para números inferiores a 2*10^6. Entre los 20 primeros son todos s_deficientes, y, según nuestras búsquedas, 30 es el único s_abundante, pues sus divisores primos suman 31: 6+10+15=31

Algunos tipos de sigma_s

Los resultados de la suma de divisores pueden presentar alguna curiosidad. Recorremos posibilidades:

Sigma_s semiprima

Si un número N es semiprimo, el valor de SIGMA_S(N) coincide con N, luego será otro semiprimo. Si no lo es, sí puede serlo SIGMA_S. Estos son los primeros ejemplos:

Observamos algo lógico, y es que las potencias de primos poseen una sigma_s semiprima, pues coincidiría con el cuadrado de ese primo. De paso hemos descubierto que existen infinitas sigmas cuadradas.

Sigma_s cuadrada

Dejamos aparte las sigmas de las potencias de primos, que son todas cuadradas, e investigamos si existen en otros casos. El resultado es

Aparecen tres números poderosos, como 225, 675 y 1125. Estos poseen todos los factores primos con exponentes superiores a la unidad, lo que explica que se esperen sigmas cuadradas.

Sigma_s prima

Por último, destacamos que aparecen bastantes sigmas primas en los primeros números, y que vuelven a aparecer números poderosos.

 

Las otras sigmas

Sumas de cuadrados

Podemos sumar los divisores semiprimos previamente elevados al cuadrado, con lo que lograríamos SIGMA2_S. Basta un pequeño ajuste en nuestras funciones, usando la operación m=m+k^2

Los primeros resultados serían

Por ejemplo, SIGMA2_S(2160)=458, porque esa es la suma de los cuadrados de sus divisores semiprimos:

4^2+6^2+9^2+10^2+15^2=458

El valor de SIGMA2_S(N) es mayor o igual al de SIGMA_S(N), lo que nos abre la posibilidad de que aquí sí existan números s2_perfectos. Y es así, porque en la tabla vemos que SIGMA2_S(16)=16. ¿Existirán más? Los buscamos, y los primeros son: 16, 81, 625 y 2401, es decir, potencias cuartas de primos, en los que su divisor semiprimo es un cuadrado de primo, y al elevarlo al cuadrado, resulta N, que así se convierte en un s2_perfecto.

Hemos acudido a la velocidad de PARI, y al menos, para números inferiores a 10^6, todos los s2_perfectos son potencias cuartas de primos:

 

Otras sigmas de potencias

Las sumas con cubos son:

 

 Igual se encontrarían para otras potencias. Lo dejamos aquí.

 

Conjunto de divisores semiprimos

(Ver entradas anteriores sobre números semiprimos)

La búsqueda de los divisores semiprimos de un número N es similar a la de los divisores primos. Aquí deberemos buscar entre todos los números menores o iguales a N, pues existen semiprimos consecutivos y no nos podemos saltar ninguno.

Una forma sencilla de identificar si un número k es divisor de N es exigir que N/k=N\k, porque entonces la división normal “/” coincidirá con la entera “\”, lo que supone que el resto de la división es cero. Si le añadimos la condición essemiprimo(k), ya los tendremos identificados.

La siguiente función construye el conjunto de divisores primos y los cuenta:

Function div_semi$(n, repe As Boolean)
Dim k, m, nn, e
Dim s$

‘La función posee el parámetro repe para detectar si un divisor puede estar elevado a una potencia

 If esprimo(n) Then div_semi = "0": Exit Function
If essemiprimo(n) Then m = m + 1: div_semi = "1 : " + Str$(n): Exit Function ‘Casos primo y semiprimo
m = 0 ‘Contendrá el número de divisores
s = ""’Será la lista de divisores
k = 4 ’Comenzamos a ensayar semiprimos
While k <= n
If essemiprimo(k) And n / k = n \ k Then ‘Es divisor semiprimo
nn = n: e = 0 ‘Posibles exponentes
If repe Then ‘Caso de repetición
While nn / k = nn \ k: e = e + 1: nn = nn / k: Wend
End If
If repe Then m = m + e Else m = m + 1
s = s + Str$(k) ‘Recoge una nueva solución
If e > 1 Then s = s + "^" + ajusta(e )’Exponente
End If
k = k + 1
Wend
s = ajusta(m) + " : " + s ‘ajusta es como Str$ sin espacio en blanco
div_semi = s
End Function

Para el caso de no contar repetidos, estos son los primeros valores. Los resultados se componen del número de divisores seguido de la lista de semiprimos:

El número de divisores está publicado en  https://oeis.org/A086971

En esa dirección figura un `programa en PARI sumamente sintético:

a(n) = sumdiv(n, d, bigomega(d)==2)

También en ella se usa otra definición de estos divisores, como aquellos semiprimos que dividen a N, pero a su cuadrado no.

La última igualdad vale 1 si es verdadera, por lo que la suma se convierte en un conteo.

Para cualquier número elegido al azar disponemos de la misma respuesta. Por ejemplo, el número 2160 posee este conjunto de divisores semiprimos: 5 :  4 6 9 10 15, es decir, 5 divisores, 4, 6, 9, 10, 15.

Podemos encontrar también la lista de divisores semiprimos contando repeticiones, si en la función anterior usamos el parámetro 1. En la siguiente tabla la hemos aplicado en números de cuatro cifras:

Los repetidos figuran con su exponente.

Versión numérica

En la función que usamos podemos concretar la salida como el número de divisores nada más. De esa forma podemos catalogar bien el objeto de la búsqueda. Por ejemplo, ¿Cuál es el primer número de cinco cifras con seis divisores semiprimos sin repetir?

Las primeras soluciones son

 

El primer número con seis divisores es el 210, y sus divisores son 6, 10, 14, 15, 21 y 35. En la dirección https://oeis.org/A220264 figuran los primeros de cada número de divisores.

Todos estos recuentos se pueden realizar a partir de la descomposición factorial del número, como un ejercicio de combinatoria elemental.

Por ejemplo, 210=2*3*5*7, y basta agruparlos por pares: 2*3=6, 2*5=10, 2*7=14, 3*5=15, 3*7=21, 5*7=35.

Si existen factores repetidos, hay que combinar con cuidado, para no repetir soluciones, En 540=2^2*3^3*5 iríamos construyendo 2*2=4, 2*3=6, 3*3=9, 2*5=10, 3*5=15.

Con la función div_semi y parámetro 0: div_semi(540;0)= 5 :  4 6 9 10 15

Nota

En el conjunto de divisores semiprimos no se puede definir un orden parcial múltiplo-divisor, ya que ningún semiprimo es múltiplo de otro. Por eso, al contrario de los divisores generales, este conjunto no forma retículo.

Puedes consultar

https://hojaynumeros.blogspot.com/2013/05/reticulos-en-el-conjunto-de-divisores-1.html y siguiente.

 

 

Semiprimos suma de los primeros

(Ver entradas anteriores sobre números semiprimos)

Cualquier número elegido al azar no tiene que ser suma de los primeros números de cierto tipo, como primos o cuadrados. Si además exigimos que ese número sea semiprimo, las posibilidades se reducen, pero tienen su interés.

Comenzamos por el caso más natural, el de los semiprimos que son suma de los primeros semiprimos.

Semiprimos

Veremos aquí los semiprimos que son suma de los primeros semiprimos hasta cierto número adecuado. La primera idea que viene a la mente es crear una columna de semiprimos  e irlos sumando. Esto es útil para visualizar los primeros, pero no nos serviría si deseáramos, por ejemplo, encontrar los primeros semiprimos con esta propiedad a partir del número 30000. En ese caso nos resultaría una tabla de excesiva extensión.

Primera soluciones

En la imagen hemos seleccionado los primeros semiprimos y en la columna siguiente los hemos sumado. Esto es sencillo en una hoja de cálculo.

Ahora habría que filtrar los semiprimos en las sumas:

En la tercera columna obtendríamos las soluciones, con unas molestas celdas vacías. Se comprende que este método no sería eficaz para tablas de más elementos. No obstante, copiamos las características de las primeras soluciones:

Por ejemplo, 58=4+6+9+10+14+15 es semiprimo, porque 58=2*29. Es curioso que los elementos 2519, 2642 y 2771 provienen de sumas consecutivas (4, 42 y 43 sumandos). Les ocurre lo mismo con 185, 219 y 254

Están publicados en https://oeis.org/A092190

Función caracterizadora

Siguiendo nuestra metodología en muchas cuestiones similares, hemos creado una función que caracteriza un número como semiprimo suma de los primeros semiprimos. Como hemos explicado, es más útil para  saber si lo cumple un número grande.

Function suma_prim_semi(n)
Dim s, k, i
Dim es As Boolean

If n < 4 Then suma_prim_semi = 0: Exit Function
s = 4 ’Suma de primeros semiprimos
i = 4 ’Número de sumandos
k = 1
es = False
While s <= n And i <= n And Not es
If s = n Then
es = True ‘Es suma
Else
i = i + 1: If essemiprimo(i) Then k = k + 1: s = s + i
End If
Wend
If es Then suma_prim_semi = k Else suma_prim_semi = 0
End Function

Con esta función podemos, por ejemplo, encontrar el primer semiprimo de este tipo con cinco cifras:  15469=31*499, suma de los 100 primeros semiprimos.

Primos

Un semiprimo también puede ser suma de los primeros primos. Basta para encontrarlos con cambiar en la función propuesta essemiprimo(i) por esprimo(i).

Los primeros elementos son:

Por ejemplo, 129 es semiprimo, pues 129=3*43 y 129 es suma de los diez primeros primos:

129=2+3+5+7+11+13+17+19+23+29

Están publicados en https://oeis.org/A189072, y en los comentarios presentan también los números de sumandos. En ella se usa el construir las sumas desde el primer primo. Este es código PARI usado:

{a=0; s=[]; forprime(p=2, 10^4, 2==bigomega(a=a+p)&s=concat(s, a)); s}

Es muy sintético, pero algo difícil de entender.

Las diferencias entre ellos siempre serán sumas de primos consecutivos, como era de esperar. Por ejemplo, 2427-2127=300=139+151.

Al igual que en el caso anterior, algunos de ellos se corresponderán con sumas consecutivas, y en ese caso, su diferencia será un número primo. Así, 77-58=19.

Cuadrados

Si en nuestra función cambiamos el ser primo o semiprimo por ser cuadrado, obtendremos los semiprimos que son suma de los primeros cuadrados. Al intentarlo nos llevamos una aparente sorpresa, y es que sólo aparecen tres soluciones:

No es tal sorpresa, si recordamos la expresión de la suma de los n primeros cuadrados:

En los ejemplos de la tabla, al dividir entre 6 el producto n(n+1)(2n+1), se elimina un factor y quedan dos, formando un semiprimo:

3*4*7/6=2*7; 5*6*11/6=5*11; 6*7*13/6=7*13

Para valores de n mayores que 6, ya no pueden quedar dos factores primos al eliminar el 2 y el 3 procedentes del denominador 6:

El producto n(n+1) es divisible entre 2,  y al ser n>6, se obtendrán dos factores, a los que habría que añadir 2n+1. Si ese producto también contiene al 3, al eliminarlo seguiríamos teniendo dos factores en n(n+1)/6, porque ni n ni n+1 son iguales a 6, y al añadir 2n+1 obtendríamos tres factores primos al menos. Nunca un semiprimo.

El factor 3 puede estar contenido en 2n+1, pero esta sería una situación aún más desfavorable para que queden dos factores primos.

Triangulares

Vista la experiencia con los cuadrados, es de esperar que en esta propuesta también obtengamos resultados limitados:

No es necesario analizarlo. Si la suma es de polinomios salvo algún denominador entero, siempre nos ocurrirá lo mismo. Por eso, no hay que intentarlo con números poligonales o piramidales.

Hipotenusas de cuaternas pitagóricas

Una cuaterna pitagórica es la expresión algebraica del teorema de Pitágoras en tres dimensiones, es decir, un conjunto de cuatro números enteros positivos a, b, c y d que cumplen:

Para estudiar bien este concepto, basta visitar, por ejemplo.

https://es.wikipedia.org/wiki/Cuaterna_pitag%C3%B3rica

https://mathworld.wolfram.com/PythagoreanQuadruple.html

En estas páginas y otras similares se encuentran todas las propiedades interesantes de estas cuaternas. Aquí nos centraremos en la hipotenusa d. Más concretamente, dado un número N cualquiera, nos interesarán las posibilidades de expresarlo como N²=a²+b²+c².

No distinguiremos entre las cuaternas primitivas y las que no lo son, ni usaremos la generalización a números enteros. Nuestro interés será más algorítmico que algebraico. Por eso, recorreremos algunas herramientas para ver sus posibilidades, sacando de cada una las propiedades oportunas.

Uso de la herramienta Cartesius

Este problema, por su carácter combinatorio implícito, es abordable con nuestra herramienta Cartesius, que produce todos los productos cartesianos de varios conjuntos sometidos a ciertas condiciones. En este caso, los conjuntos son tres, formados por los primeros cuadrados, para representar a a², b² y c², y la condición es que su suma coincida con N². Lo explicaremos con un ejemplo, el de N=35.

Para resolver la cuestión emplearemos las siguientes condiciones:

Las estudiamos una a una:

xtotal=3

Indica que combinaremos tres conjuntos. Aquí serían a², b² y c²

xt=1..1224

Damos una cota a cada conjunto de 35²-1=1224, para evitar ceros

xt=filtro(cuadrado)

Cada conjunto se restringirá a los cuadrados

suma=1225

La suma deberá ser 35²

Creciente

Se exigen soluciones con los términos crecientes para evitar repeticiones.

Con el botón Iniciar, o el Reiterar de la siguiente hoja “Producto” obtenemos todas las soluciones.

Resultan cinco posibilidades, pero expresadas como cuadrados. Como las hojas de cálculo te permiten retoques posteriores, bastará usar la función RAIZ para encontrar sus bases, los valores de a, b y c. Incluso se pueden cambiar los rótulos y los fondos:

Hay que advertir, antes de seguir, que en un equipo informático doméstico estos cálculos pueden tardar, en esta época en la que deseamos respuestas rápidas. Todo lo que implique desarrollos combinatorios se ralentizará inevitablemente.

Cartesius es una herramienta potente y de resultados claros, aunque la redacción de las condiciones puede resultar compleja. Por eso existe una Guía para su uso en

http://www.hojamat.es/sindecimales/combinatoria/herramientas/cartesius.pdf

Si deseamos más versatilidad, como efectuar el recuento de las soluciones, expresarlas en modo texto o aplicarles un Buscador, es preferible acudir, como hemos decidido tantas veces, a la construcción de una función en VBasic, para su uso en Excel y Calc.

Función de búsqueda

Function espitag3(n) As String ‘Da como solución un texto
Dim k, p, d, k1, p1, d1, cuenta
Dim s$

s = "" ‘Contenedor de la solución
cuenta = 0 ‘Número de soluciones
k = 1: p = 3 ‘Variables para formar cuadrados
While k <= n * n / 2
d = n * n – k ‘N^2 menos el primer cuadrado
k1 = 1: p1 = 3 ’Inicio del segundo cuadrado
While k1 <= d / 2
d1 = d - k1
If escuad(d1) And d1 >= k1 And k1 >= k Then ‘Hay solución
s = s + " ## " + Str$(Sqr(k)) + "^2+" + Str$(Sqr(k1)) + "^2+" + Str$(Sqr(d1)) + "^2 " ‘Añade una solución
cuenta = cuenta + 1’Incrementa la cuenta
End If
k1 = k1 + p1: p1 = p1 + 2 ‘Avanza el primer cuadrado
Wend
k = k + p: p = p + 2 ‘Avanza el segundo cuadrado
Wend
If s = "" Then s = "NO"
espitag3 = Str$(cuenta) + " : " + s
End Function

Hay que explicar que los dos primeros sumandos cuadrados se generan sumando números impares. Para ello se usa la variable k para contenerlos, y la variable p para los incrementos. Así, para iniciar el primer cuadrado declaramos k=1,p=3, con lo que el primero es 1^2 y el segundo 1+3=2^2. Terminado de analizar un cuadrado, k se incrementa en p, k=k+p, y p se incrementa en 2 para seguir con los impares.

Al final del proceso se inserta la cuenta de soluciones al principio del texto.

Aplicamos esta función al 35:

Obtenemos que son cinco soluciones, y se presentan ya en forma de suma por si las deseamos copiar en otras celdas. Como era de esperar, coinciden con las cinco obtenidas con Cartesius.

El que la suma figure en primer lugar nos permite búsquedas de números con un número determinado de descomposiciones pitagóricas de este tipo. Por ejemplo, en esta tabla figuran aquellos números que admiten dos descomposiciones:

Algoritmo en PARI

Podemos traducir todo al lenguaje PARI. No es fácil de entender el código, que presenta una ventaja, además de funcionar más rápidamente, y es que imprime también las bases de los cuadrados, pero el resultado de la función es la cuenta de las descomposiciones, lo que facilita las búsquedas. En las siguientes líneas puedes consultar el programa creado para encontrar números con descomposición única:

pitag3(n)={my(k=1,p=3,cuenta=0,d,k1,p1,d1);while(k<=n*n/2,d=n*n-k;k1=1;p1=3;while(k1<=d/2,d1=d-K1;if(issquare(d1)&&d1>=k1&&k1>=k,print(sqrtint(k),", ",sqrtint(k1),", ",sqrtint(d1));cuenta+=1);k1=k1+p1;p1=p1+2);k=k+p;p=p+2);cuenta}

for(i=1,1000,if(pitag3(i)==1,print1(i,", ")))

Obtendremos el resultado

En https://oeis.org/A152829 figuran esos números que sólo admiten una solución. Contiene una conjetura de Colin Baker de que, a partir del 13, se cumple que a(n)=2a(n-3). Se puede comprobar en el listado: 26=2*13, 28=2*14, 48=2*24,…

Lo curioso es que en nuestra sucesión de dos descomposiciones también se puede enunciar la misma conjetura:

11, 17, 22, 25, 34, 44, 50, 68, 88, 100,…

En ella 34=2*17, 44=2*22,…

Lo que llama la atención no es que sea el doble, que algo similar ocurre en las ternas pitagóricas, en las que se pueden multiplicar todos los sumandos por un mismo factor, sino que no se interpongan otras soluciones entre un elemento y su doble, además de los dos de la conjetura.

¿Ocurrirá también con los que presentan tres soluciones? Lo vemos:

Efectivamente, ocurre, pero con un salto de cinco en lugar de tres: 30=2*15, 36=2*18,…, es decir, a(n)=2a(n-5)

Goldbach con semiprimos

(Ver entradas anteriores sobre números semiprimos)

Al igual que en la conjetura de Goldbach, que descomponemos todo número par en suma de dos primos, aquí podemos intentar un proceso igual con semiprimos, pero sin la condición de que el número sea par. Después intentaremos pasar a más sumandos.

Suma de dos semiprimos

No es difícil, si se posee la función ESSEMIPRIMO, descomponer un número en suma de semiprimos. Además, si consultamos https://oeis.org/A072931,  descubriremos que suelen aparecer soluciones múltiples. Por eso, nos conviene crear una función que devuelva todas las soluciones en modo texto y que se inicie con el número de ellas, para poder abordar búsquedas especiales. Hemos elegido esta:

Function suma2semi$(n)
Dim k, m
Dim s$

m = 0 ‘Número de soluciones
s = "" ’Contenedor de soluciones
For k = 4 To n / 2
If essemiprimo(k) And essemiprimo(n - k) Then
m = m + 1 ‘Hay una nueva solución
s = s + " ## " + ajusta(k) + "+" + ajusta(n - k)
‘ajusta es idéntica a Str$ pero sin espacio
End If
Next k
If m > 0 Then s = ajusta(m) + s ‘Se inserta número de soluciones
suma2semi = s
End Function

Con ella es fácil descomponer un número natural en suma de dos semiprimos. Por ejemplo, en el caso de 88, las soluciones son:

5 ## 6+82 ## 14+74 ## 26+62 ## 33+55 ## 39+49

Vemos que son sólo cinco, como indica el primer dígito

Uso de Cartesius

Nuestra herramienta Cartesius también permite buscar los dos sumandos semiprimos (Descargable desde http://www.hojamat.es/sindecimales/combinatoria/herramientas/herrcomb.htm#cartesius)

En este primer recorte de pantalla podemos observar el planteamiento:

Exige que sean dos los sumandos, desde 1 hasta 88, les aplica el filtro SEMIPRIMO, que la suma sea 88 y sólo devuelve soluciones crecientes, para evitar duplicidades. El resultado lo tenemos en la siguiente captura:

Coincide con los cinco resulatdos obtenidos mediante la función, pero esta es más flexible para búsquedas, por lo que Cartesius nos sirve preferentemente para comprobar.

Números no descomponibles

Si establecemos una búsqueda con la exigencia de que el resultado de la función sea una cadena vacía, obtendremos aquellos números que no admiten esta descomposición en dos semiprimos. El resultado es:

Están publicados en https://oeis.org/A072966, y en ella, T,D, Noe sugiere que no hay más números sin la descomposición exigida (conjetura).

Para más rapidez de cómputo, hemos creado este código en PARI, que determina tan sólo si existe o no suma de dos semiprimos:

sumasemi(n)={my(m=0,k=4);while(k<=n/2&&m==0,if(bigomega(k)==2&&bigomega(n-k)==2,m=1);k+=1);m}

for(i=1,10^4,if(sumasemi(i)==0,print(i)))

Hemos establecido una búsqueda hasta 10000 sin encontrar más soluciones:

Números con más descomposiciones

En la sucesión https://oeis.org/A072931 no aparecen más de 8 soluciones por número. Con nuestras herramientas podemos intentar encontrar los primeros enteros con 8 descomposiciones o más:

Se encuentran tantas, que se comprende la conjetura del 33 como último número sin soluciones.

El primer número con veinte descomposiciones es el 320. Se entiende entonces que no hay que avanzar mucho para que el número de soluciones aumente velozmente.

Descomposición en tres semiprimos

Se puede ampliar la función SUMA2SEMI a tres sumandos, con lo que resulta un código algo más complejo, porque hemos procurado que los sumandos sean crecientes. Lo copiamos para que su estudio sea algo opcional:

Function suma3semi$(n)
Dim k, m, j, b
Dim s$

m = 0
s = ""
For k = 4 To n
If essemiprimo(k) Then
b = n - k
If b >= k Then
For j = 4 To b
If essemiprimo(j) And essemiprimo(b - j) Then
If b - j >= j And j >= k Then
m = m + 1
s = s + " ## " + ajusta(k) + "+" + ajusta(j) + "+" + ajusta(b - j)
End If
End If
Next j
End If
End If
Next k
If m > 0 Then s = ajusta(m) + s
suma3semi = s
End Function

Con esta función obtenemos las descomposiciones de los primeros números naturales. Hasta el 12 no hay descomposiciones, ya que 12=4+4+4 es la mínima suma. El 13 y el 15 tampoco presentan sumas de tres semiprimos. Los siguientes ya presentan una o varias sumas:

Se puede conjeturar, al igual que en el caso de dos sumandos, que los números siguientes presentarán todos una solución al menos.

Con Cartesius se comprueban estos cálculos:

Incluimos como ejemplo un planteo para el 29:

Resultado:

Se confirma lo obtenido con la función.

No merece la pena pasar a más sumandos, pero con Cartesius podemos abordarlo para un ejemplo concreto, pero suele tardar mucho el proceso en cuanto aumentamos el número de soluciones. Como ejemplo, incluimos las descomposiciones del número 30 en cuatro semiprimos:

 

Semiprimos con plantilla

(Ver entradas anteriores sobre números semiprimos)

Los semiprimos del tipo N=pq admiten otros condicionamientos, a los que llamaremos “plantillas”. Por ejemplo, semiprimos del tipo p(p+4). Los de tipo p(p+2), producto de dos primos gemelos, se estudian en otra parte de esta publicación.

N=p(p+4)

Los pares de primos p y p+4 son llamados “cousin” en inglés. En nuestro idioma, lo de “primos primos” no suena bien, pero así se designan en la Wikipedia.

Búsqueda directa

Con el Buscador hemos organizado las condiciones de forma que las soluciones caen en la segunda columna:

Al ser 4 la diferencia entre los dos factores, ambos serán del tipo 4k+1 o bien del 4k+3. En el primer caso, el semiprimo se podrá descomponer en dos sumas de cuadrados, como le ocurre al 12317=109*113, que admite estas dos:

12317=94^2+59^2=101^2+46^2

En los otros casos, como el 4757, no admitirán descomponerse en suma de dos cuadrados, por ser sus factores del tipo 4k+3.

Ayuda algebraica

Para encontrar el valor de p de forma directa nos basamos en dos desigualdades:

N=p(p+4)=p²+4p<p²+4p+4=(p+2)²

N=p(p+4)=p²+4p>p²+2p+1=(p+1)²

Según esto, p será la parte entera de la raíz cuadrada de N menos una unidad:

Por ejemplo, lo aplicamos a 16637, con el lenguaje de las hojas de cálculo:

p=ENTERO(RAIZ(16637)-1)=127, lo que es correcto, porque 16637=127*131

Esto nos permite reconocer semiprimos del tipo p(p+4) sin tener que recorrer los posibles divisores de N. Basta encontrar p, exigir que p y p+4 sean primos y que su producto sea igual a N.

Con este procedimiento hemos averiguado en un tiempo de cálculo razonable, que entre 1000000 y 1100000 solo existe un semiprimo de este tipo:

1022117=1009*1013

Más álgebra

Aún podemos concretar mejor las búsquedas de estos semiprimos. Con este desarrollo lo aclararemos muy bien:

N=pq=p(p+4)=p²+4p

Es fácil ver, según esto, que N+4 es un cuadrado, luego para buscar N podemos restringirnos a los números que equivalen a k²-4 para un valor adecuado de k. Así que, en cualquier búsqueda nos dedicaremos a aquellos números de este tipo, con el consiguiente ahorro de tiempo. Además, si escribimos la equivalencia como p²+4p-N=0, podemos hallar p de forma directa. Sería:

Al ser 4+N cuadrado, la solución es entera, como era de esperar.

Esto simplifica la búsqueda, pues comenzamos por exigir que 4+N sea cuadrado perfecto. Después calculamos p con la fórmula anterior, y bastará exigir que tanto p como p+4 sean primos.

Así lo hemos efectuado en esta búsqueda, en el intervalo (10000,50000):

Como era de esperar, las soluciones coinciden con las obtenidas con otros métodos.

Prescindimos del cuadrado

Si lo que nos interesa es conseguir una lista de soluciones a partir de la unidad, podemos prescindir del carácter de cuadrado de N+4, ya que podemos crear una variable k=1 e irle sumando los impares en cada paso, con lo que se irán construyendo los cuadrados, pues 1+3=4, 4+5=9, 9+7=16,…

Así lo hemos construido en PARI, y nos devuelve, por ejemplo, todas las soluciones menores que 10^6 de forma casi instantánea en su aplicación GP/PARI CALCULATOR, y con cierta rapidez en su web

 https://pari.math.u-bordeaux.fr/gp.html

El código es

k=1;d=3;tope=10^6;while(k<=tope,k=k+d;n=k-4;p=-2+sqrtint(k);if(isprime(p)&&isprime(p+4),print(k-4,", ",p,", ",p+4));d+=2)

El tope, fijado en 10^6, se puede cambiar según sean nuestros objetivos. Los primeros resultados son:

 

Caso general

Los razonamientos útimos sobre el tipo de semiprimo p(p+4) se generalizan fácilmente a N=p(p+2k). Nos limitamos a traducirlos:

N ha de ser del tipo m²-k², para un valor de m adecuado. Expresado de otra forma, N+k² ha de ser cuadrado, y al tener raíz cuadrada entera, nos permite despejar p:

Después de este cálculo, basta exigir que tanto p como p+2k sean primos.

Como ejemplo, buscamos todos los semiprimos del tipo p(p+12) entre 10000 y 50000:

 

Por último, estos serían los primeros de seis cifras del tipo p(p+20):

 

 Ha sido entretenido el estudio. Lo dejamos aquí.

Otras plantillas

El tema de plantillas de tipo polinómico es muy extenso, por lo que sólo estudiaremos algunas más como ejemplo.

N=p(2p+1)

Comenzamos con el Buscador para ir iniciando el estudio con algo intuitivo.

Los semiprimos aparecen en la columna de Detalles.

Es claro que p es un primo de Sophie Germain y 2p+1 un primo seguro.

Están publicados en

 https://oeis.org/A156592:

10, 21, 55, 253, 1081, 1711, 3403, 5671, 13861, 15931, 25651, 34453, 60031, 64261, 73153, 108811, 114481, 126253, 158203, 171991, 258121, 351541, 371953, 392941, 482653

Todos estos semiprimos son números triangulares de orden par. La razón es que se pueden escribir como 2n(2n+1)/2=T(2n).

Esta propiedad nos facilita el trabajo, porque un criterio previo sería que N fuera triangular, y tenemos un criterio adecuado, y es que 1+8N sea un cuadrado. En realidad, si no se conociera este criterio, aparecería de forma natural con alguna manipulación algebraica. En efecto, se cumplirá siempre que

2p²+p-N=0

Despejamos p y resulta:

 

Luego para identificar estos números hay que comenzar con que 1+8N sea cuadrado y el numerador múltiplo de 4.

Todo este desarrollo se justifica porque para manejar números grandes no sería eficiente comenzar por la unidad, como hemos procedido con el Buscador, sino que es más útil calcular el valor de p si se cumplen las condiciones.

Así que debemos proceder por verificar los criterios, el de que 1+8N sea cuadrado y el que el valor de p sea entero (en realidad, basta con lo segundo, pero así queda más claro). Después verificaríamos si tanto p como p+2k son primos:

En Vbasic exigiríamos

D=1+8N
P=(-1+RAIZ(D))/4
ESCUAD(D) AND ESENTERO(P)

Después vendría el que tanto P como 2P+1 sea primos.

Procediendo así, obtenemos los mismos resultados que con el Buscador:

Es cierto que este método es muy útil para búsquedas de números grandes. En la imagen puedes consultar el primer semiprimo de este tipo a partir de 10^6:

Plantilla general

Con el ejemplo de los primos de Sophie Germain nos basta para entender el procedimiento adecuado si el segundo primo es función lineal del primero.

Para una plantilla general del tipo N=p(ap+b) ya sabemos cómo proceder:

Planteamos ap²+bp-N=0

Despejamos p:

 

Exigimos que p sea entero, lo que implica que el discriminante sea cuadrado. Si esto se cumple, verificamos que tanto p como ap+b sean primos.

Por ejemplo, buscamos semiprimos de la forma

N=p(3p+2)

Abrimos camino con el Buscador:

 

La ecuación de segundo grado en p sería, en este caso,

3p²+2p-N=0

El discriminante 4+12N ha de ser cuadrado

La solución de la ecuación p ha de ser entera y número primo, así como 3p+2

Con esas condiciones podemos encontrar los semiprimos pedidos:

Hemos realizado la búsqueda entre 50000 y 100000: